一道有趣的路径规划算法题（Java 版）

问题

图中有一个无向图，其中圈内数字代表一个地点，边线上的数字代表长度 Le（双向相同）。机场一辆小型VIP电动摆渡车在起点 A，要去 3 个贵宾厅（V1，V2，V3）接贵宾（每个贵宾厅限1个VIP），送到 3 个对应航班机位（S1，S2，S3），即 V1 至 S1，V2 至 S2，V3 至 S3。VIP 电动摆渡车同时最多装下 2 个 VIP。

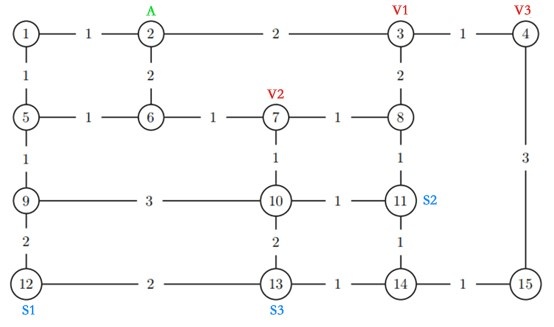
要求：VIP 电动摆渡车该怎么走路径最短？这个最短路径的长度是多少？这里 A 是出发点，最后一个 VIP（不限次序）送达地为终点。为了简化问题，假设贵宾厅VIP已在贵宾厅等候上车，VIP 电动摆渡车在接送期间不用等待。

分析

看到最短路径，不难想到 Dijkstra 等最短路径算法，这些算法用于求出一个图（Graph）中任意两个顶点（Vertex）的最短距离。但是本文待求解的问题不止于此，而是包含起始点 A 在内的 7 个点（A、V1、V2、V3、S1、S2、S3），我们需要先规划路线使得摆渡车依次通过这 7 个点，再求出这些路线中的最短路线。

综上所诉，该问题被拆解为以下两步：
第一步，列出从 A 出发经由其余 6 个点的所有可能的路线。
第二步，对于给定的任意两个点，求出它们之间的最短路径（例如给定 A、V2 两个点，可得从 A 到 V2 的最短路径为 2 -> 6 -> 7）。
然后对于每条路线，计算每一段（即两个点之间）的最短路径即可得到整条路线的最短路径。

由此，可以看出本题涉及两个算法，即第一步中的排序算法，和第二步中的最短路径算法。

排序算法

我们需要对 V1、V2、V3、S1、S2、S3 六个点进行排序。当然为满足题目的要求，排序得出的路线必须满足以下几个条件：

第一个点必须是 V，最后一个点必须是 S
因为摆渡车最多载两个，所以不能出现连续的三个 V
为确保将用户送达目的点，对应的 V 不能排在对应的 S 后面，比如不能排出 S1 … V1

建模

Point，枚举类，对应着包括起点 A 在内的七个点。阔号中的整数类型表示点在图中的索引。同时基于 Java 面向对象的思想，赋予它一些验证方法以验证当前路径是否符合上述三个条件。

public enum Point {
    A(2, START),
    V1(3, VIP),
    V2(7, VIP),
    V3(4, VIP),
    S1(12, DESTINATION),
    S2(11, DESTINATION),
    S3(13, DESTINATION);

    private final int index;
    private final Type type;

    public int index() { return index; }

    public boolean isV() { ... }

    public boolean isS() { ... }

    public Point matchedV() { ... }

    public enum Type {
        VIP, DESTINATION, START
    }
    
    // ...
}

Route，对应着路线，下面粘贴了部分代码，包括验证当前路线是否合法的 isLegal() 方法，路径上追加点的 add(Point) 方法，以及预留的 minDistance() 方法用于计算这条路径的最短距离。

public class Route {
    private final List<Point> route;
    
    public boolean isLegal() { ... }   
    public void add(Point point) { ... }
    public int minDistance() { ... }
    ...
}

算法实现

排序算法的核心思路是：

首先需要一个容器用于所有装符合条件的 Route。
Route 用来装当前已入队列的 Point。
Remain Points Container 用于存放尚未入队列的 Point。
从 Remain Points Container 依次拿出一个 Point，追加入 Route，判断是否合法，合法则继续，不合法则退出。
第 4 步是一个递归的步骤，如下图，假设第一个点装入了 V1，第二个点在装入的时候可以装入 V2、V3、S1、S2、S3，其中 S2、S3 因为不合法而终止递归，剩下的 V2、V3、S1 三个点 fork 出三种情况继续向下递归。
直到 Route 将六个点全部装入后，将该 Route 加入第 1 步的容器中。

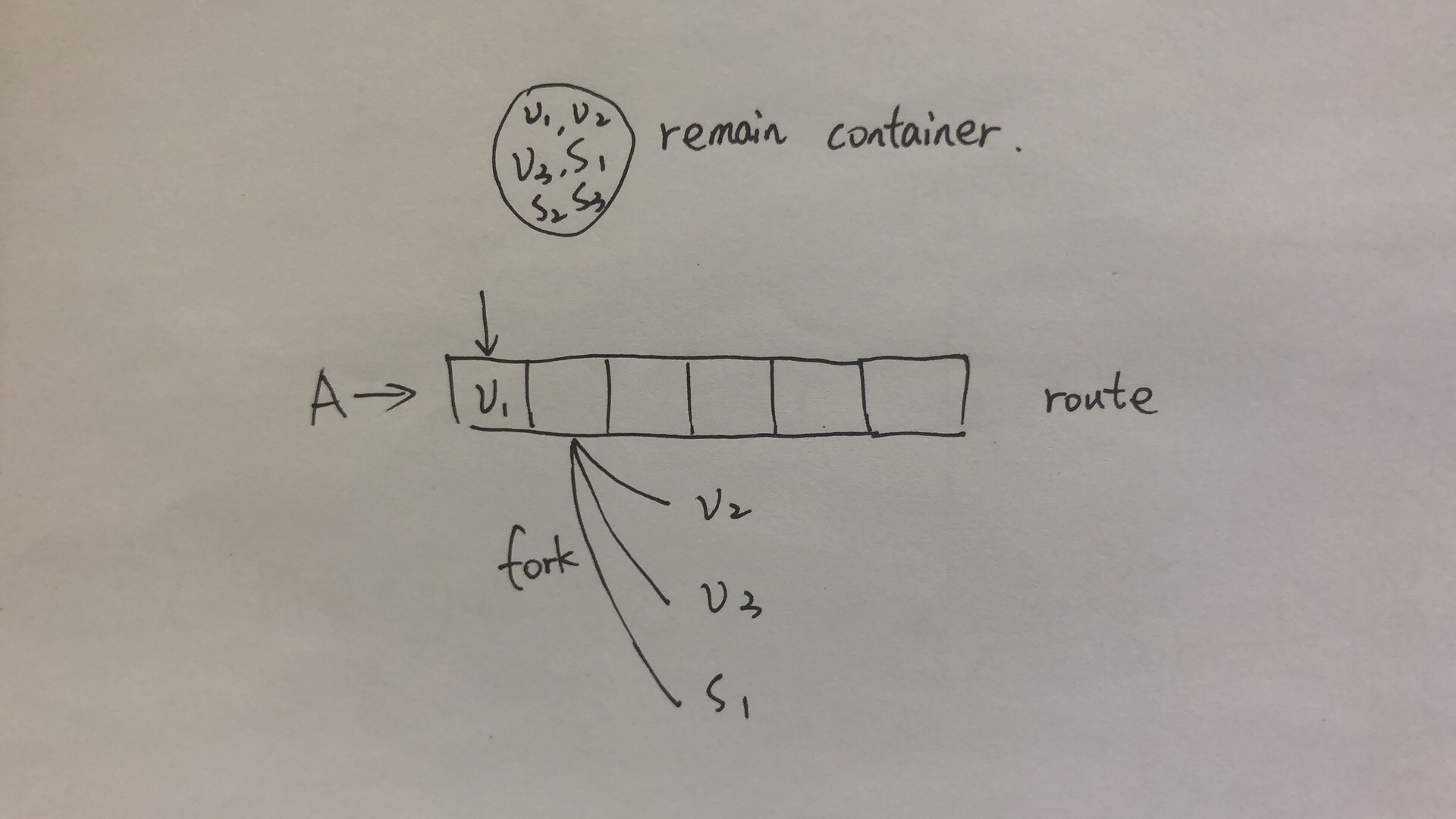
RouteGenerator 类，用于生成所有符合条件的路线。

public class RouteGenerator {
    private List<Route> routes = new ArrayList<>(); // 第 1 步的容器

    public List<Route> generate() {
        fork(new Route(), List.of(V1, V2, V3, S1, S2, S3));
        return routes;
    }

    private void fork(final Route route, final List<Point> remain) { // 入参分别对应 2、3 步
        if (!route.isLegal()) { // 判断是否合法，不合法则中断递归
            return;
        }

        if (route.size() == 6) { // 当六个点全部装入后，将该路线加入第 1 步的容器并中断递归
            routes.add(route); 
            return;
        }

        for (int i = 0; i < remain.size(); i++) {
            List<Point> temp = Lists.newArrayList(remain);
            Point next = temp.remove(i); // 从未入队列的点中选出一个加入路线
            Route route1 = route.copy();
            route1.add(next);

            fork(route1, temp); // 递归调用
        }
    }
}

运行结果

排序后得到结果，一共 54 种符合条件的情况。算法耗时在 40ms 左右。该算法相较于全排列后再进行筛选，可以避免创建不必要的对象。

A -> V1 -> V2 -> S1 -> V3 -> S2 -> S3
A -> V1 -> V2 -> S1 -> V3 -> S3 -> S2
A -> V1 -> V2 -> S1 -> S2 -> V3 -> S3
...
A -> V2 -> V3 -> S3 -> V1 -> S1 -> S2
A -> V2 -> V3 -> S3 -> V1 -> S2 -> S1
A -> V2 -> V3 -> S3 -> S2 -> V1 -> S1
...
A -> V3 -> S3 -> V2 -> V1 -> S1 -> S2
A -> V3 -> S3 -> V2 -> V1 -> S2 -> S1
A -> V3 -> S3 -> V2 -> S2 -> V1 -> S1

最短路径算法

本题中的最短路径算法我选用的 Dijkstra 算法，亦就是大学数据结构课程中最为常知的最短路径算法。算法的详细步骤这里就不再赘述了，可以参考一篇博客 Dijkstra最短路算法。

建模

Dijkstra 算法的核心建模思想是使用一个二维数组，记录每个顶点到其他顶点的距离，如果不能直达，则设为 ∞。那么本题的图可以使用如下二维数组来表示，由于是无向图，所以关于对角线对称。

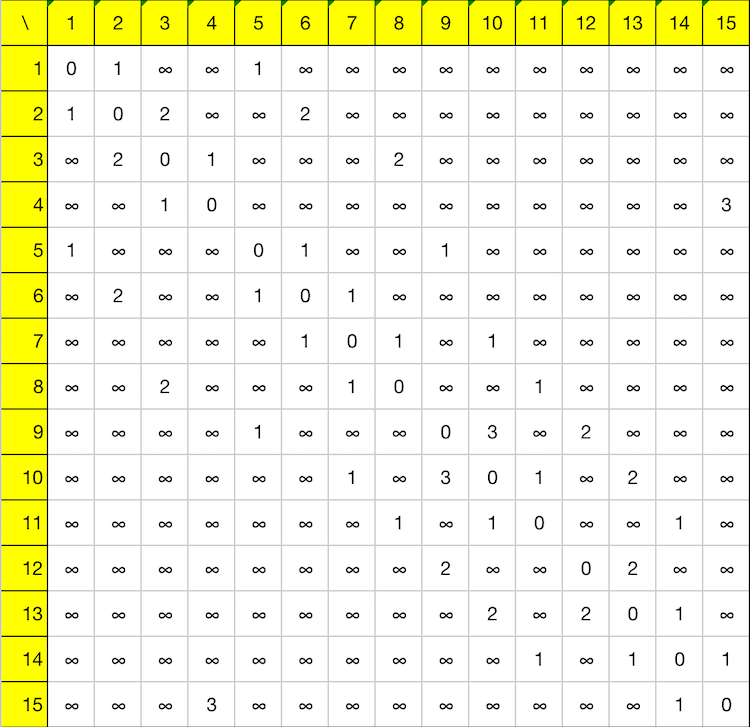
反应在 Java 代码中则是如下：

public class Graph {
    private static final int I = Integer.MAX_VALUE;
    public static final int INFINITY = I;

    // todo: maybe read from graph with python
    public int[][] matrix() {
        return new int[][]{
//               1  2  3  4  5  6  7  8  9  10 11 12 13 14 15
                {0, 1, I, I, 1, I, I, I, I, I, I, I, I, I, I}, // 1
                {1, 0, 2, I, I, 2, I, I, I, I, I, I, I, I, I}, // 2
                {I, 2, 0, 1, I, I, I, 2, I, I, I, I, I, I, I}, // 3
                {I, I, 1, 0, I, I, I, I, I, I, I, I, I, I, 3}, // 4
                {1, I, I, I, 0, 1, I, I, 1, I, I, I, I, I, I}, // 5
                {I, 2, I, I, 1, 0, 1, I, I, I, I, I, I, I, I}, // 6
                {I, I, I, I, I, 1, 0, 1, I, 1, I, I, I, I, I}, // 7
                {I, I, 2, I, I, I, 1, 0, I, I, 1, I, I, I, I}, // 8
                {I, I, I, I, 1, I, I, I, 0, 3, I, 2, I, I, I}, // 9
                {I, I, I, I, I, I, 1, I, 3, 0, 1, I, 2, I, I}, // 10
                {I, I, I, I, I, I, I, 1, I, 1, 0, I, I, 1, I}, // 11
                {I, I, I, I, I, I, I, I, 2, I, I, 0, 2, I, I}, // 12
                {I, I, I, I, I, I, I, I, I, 2, I, 2, 0, 1, I}, // 13
                {I, I, I, I, I, I, I, I, I, I, 1, I, 1, 0, 1}, // 14
                {I, I, I, 3, I, I, I, I, I, I, I, I, I, 1, 0}, // 15
        };
    }
}

算法实现

Dijkstra 算法的核心思想是：每次找到离源点最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。基本步骤如下：

使用一个 dis[] 数组记录源点到其余所有点的最短路径。初始化为 matrix 二维数组的对应行。
将所有的顶点分为两部分：已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始，已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个 book[] 数组来记录哪些点在集合 P 中。例如对于某个顶点 i，如果 book[i] 为 1 则表示这个顶点在集合 P 中，如果 book[i] 为 0 则表示这个顶点在集合 Q 中。
在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u（即 dis[u] 最小）加入到集合 P。并考察所有以点 u 为起点的边，对每一条边进行松弛操作。例如存在一条从 u 到 v 的边，使得 s -> u -> v 的长度 dis[u] + e[u][v] 比目前已知的 dis[v] 的值更小，那么我们就可以用新值来更新当前 dis[v] 中的值（即松弛）。
重复第 3 步，如果集合 Q 为空，算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径。

public class Dijkstra {
    private final int[][] e;

    public Dijkstra(Graph graph) {
        this.e = graph.matrix();
    }

    public int min(int start, int end) {
        int n = e[0].length;

        // init dis[]
        int[] dis = new int[n];
        System.arraycopy(e[start - 1], 0, dis, 0, n);

        // init book[]
        int[] book = new int[n];
        book[0] = 1;

        for (int i = 0; i < n - 1; i++) {
            int min = INFINITY;
            int u = 0;
            for (int j = 0; j < n; j++) {
                if (book[j] == 0 && dis[j] < min) {
                    min = dis[j];
                    u = j;
                }
            }
            book[u] = 1;
            for (int v = 0; v < n; v++) {
                if (e[u][v] < INFINITY) {
                    if (dis[v] > dis[u] + e[u][v]) {
                        dis[v] = dis[u] + e[u][v];
                    }
                }
            }
        }

        return dis[end - 1];
    }
}

其中 Dijkstra 算法我有想过使用缓存 Cache 去进行优化，为了避免重复计算两个点之间的最短距离，但实际上效果反而不好，其实这是一种空间换时间的取舍，虽然不用重复计算，但是需要额外的空间存储已计算过的路径。然而在本题中并不适用这种优化。

运行结果

结合 Dijkstra 算法，我们可以补全之前 Route 类中预留的 minDistance() 方法的实现：

// Route.class
public int minDistance() {
    AtomicReference<Point> pre = new AtomicReference<>(Point.A);
    return route.stream()
            .map(p -> {
                int min = dijkstra.min(pre.get().index(), p.index());
                pre.set(p);
                return min;
            })
            .reduce(0, (i1, i2) -> i1 + i2);
}

最后在主方法中运行可得答案，运行耗时在 100ms 左右。

public static void main(String[] args) {
    long before = System.currentTimeMillis();

    List<Route> routes = new RouteGenerator().generate();
    routes.forEach(route -> System.out.println(route + " 最短路径长度: " + route.minDistance()));
    Route shortestRoute = routes.stream().min(Comparator.comparing(Route::minDistance)).get();
    System.out.println(String.format("\n其中最短路径为 %s, 路径长度为 %s.", shortestRoute, shortestRoute.minDistance()));

    long after = System.currentTimeMillis();
    System.out.println("运行耗时:" + (after - before) + "ms.");
}

// 其中最短路径为 A -> V2 -> S2 -> V1 -> V3 -> S3 -> S1, 路径长度为 16.
// 运行耗时:108ms.

总结

本文主要是想向大家展示 Java 面向对象处理问题的优势。虽然可能代码量会多一些，但是在重构和梳理编码过程的时候，这种面向对象的思想无疑会带来很多好处。例如本文中 Route、Point、Graph 这些类的建模相较于面向过程编码更符合人的直觉；以及为避免贫血对象，我们赋予类丰富的行为，例如一些验证方法、minDistance() 等方法；同时还要多写单元测试，这样可以随时验证算法的正确性，而不用等到编码完成的最后再去肉眼比对结果。

代码已经上传到 GitHub 上，包含了相对全面的单元测试，需要注意的是使用的 Java 11 版本。以后可能会使用 Python 编码实现，再比较两种语言的优劣势。