什么是二分图
定义:设 G=(V, E) 是一个无向图,如果顶点 V 可分割为两个互不相交的子集{U}、{V},并且图中的每条边 (i, j) 所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集 i∈ U,j∈ V,则称图 G 为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。
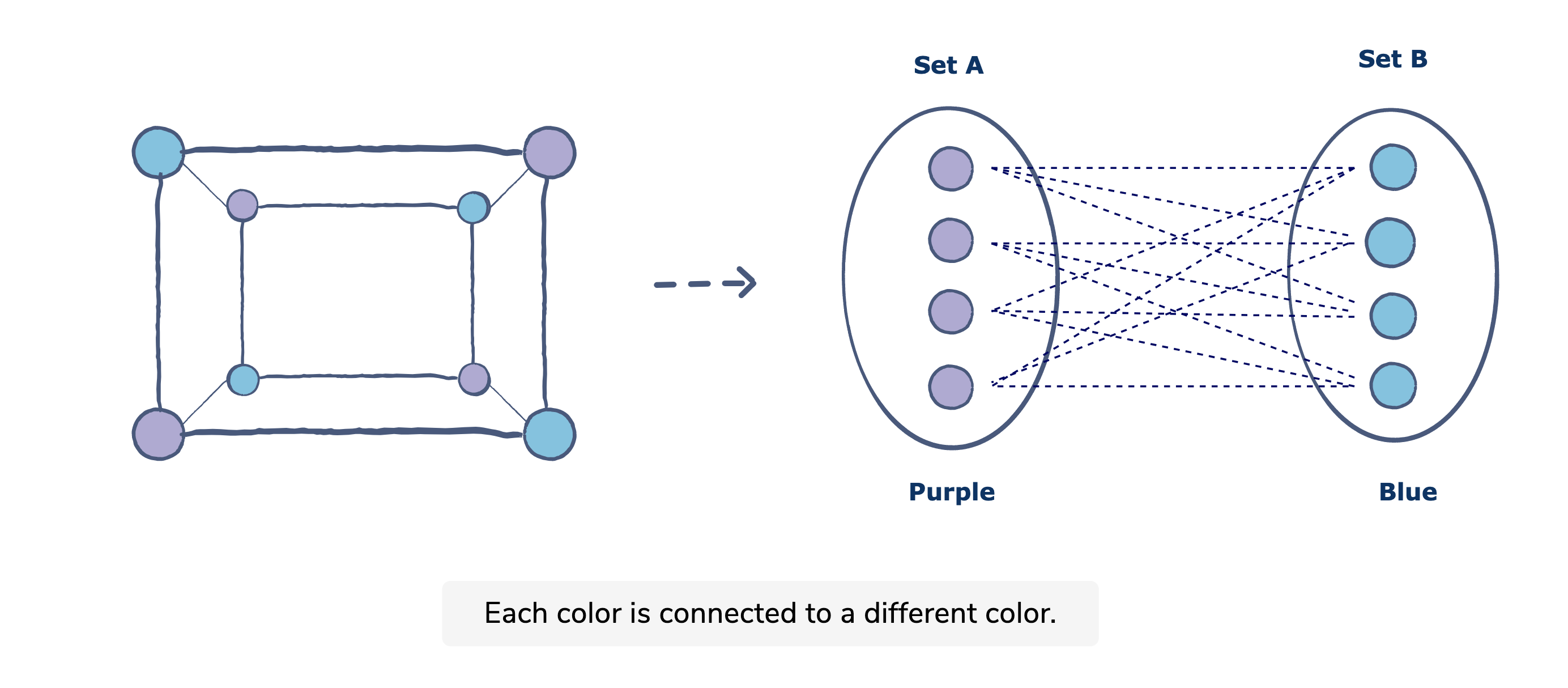
二分图(Bipartite Graph)是指图中的顶点可以划分到两个不相交的集合中,同一个集合中的顶点不相邻,即同一个集合中的两个顶点之间不存在边。如下图,我可以将左侧的蓝色和紫色构成的图转化为右图的二分图,集合 A 中全由紫色顶点构成,集合 B 中全由蓝色顶点构成,只存在蓝-紫(紫-蓝)边,同色顶点间不存在边。
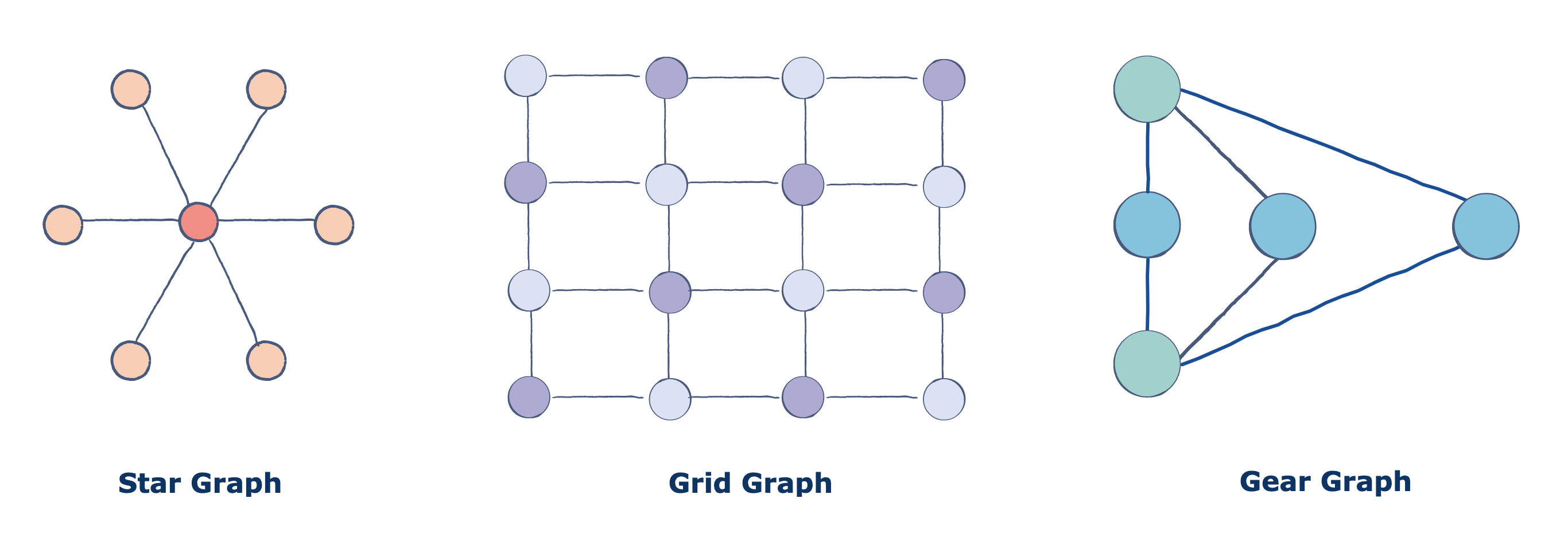
所以二分图又可以等价于二色图(Two-colorable Graph),以下是一些二分图的常见示例,如星状图、网格图、齿轮图等。
Bipartiteness Check
批处理
那么如何检测一个图是否为二分图呢?在批处理情形下,即一个图的所有顶点和所有边的信息都已明确,我们借助于二色图的思想,可以通过染色法来判断一个图是否为二分图。算法可以通过 BFS 广度优先算法来实现,具体步骤如下:
- 从任意一个顶点出发,将该顶点染成黑色。
- 遍历该顶点的所有相邻顶点,将其染成白色。
- 采用 BFS 依次遍历各个顶点的相邻顶点,将其染成与自身颜色相反的颜色。
- 当出现已访问过的相邻顶点颜色与自己相同,则该图不是二分图。否则,该图为二分图。
流处理
在流处理情形下,我们无法预知图的所有信息,取而代之的是,图的边(Edge)作为输入持续不断的流入我们的系统中。在这种情况下,考虑如何实时地判断当前所有边构成的图是否为二分图?
我们可以参考 GitHub 上的 Gelly Streaming 项目,该项目是 Flink 的一个轻量级图流处理 API,提供了一些图流分析接口,并实现了部分图的流处理算法。
Gelly Streaming 的算法核心思想仍然是染色法,具体步骤如下:
- 在一条边进入系统时,如果该边是已经存在的边,则丢弃;如果该边的两个顶点均不存在,则将其染成两个不同的颜色;如果该边有且仅有一个顶点已存在(已染色),则将另一个顶点染成相反的颜色。
- 如果该边的两个顶点均已存在,则可能出现三种情况:
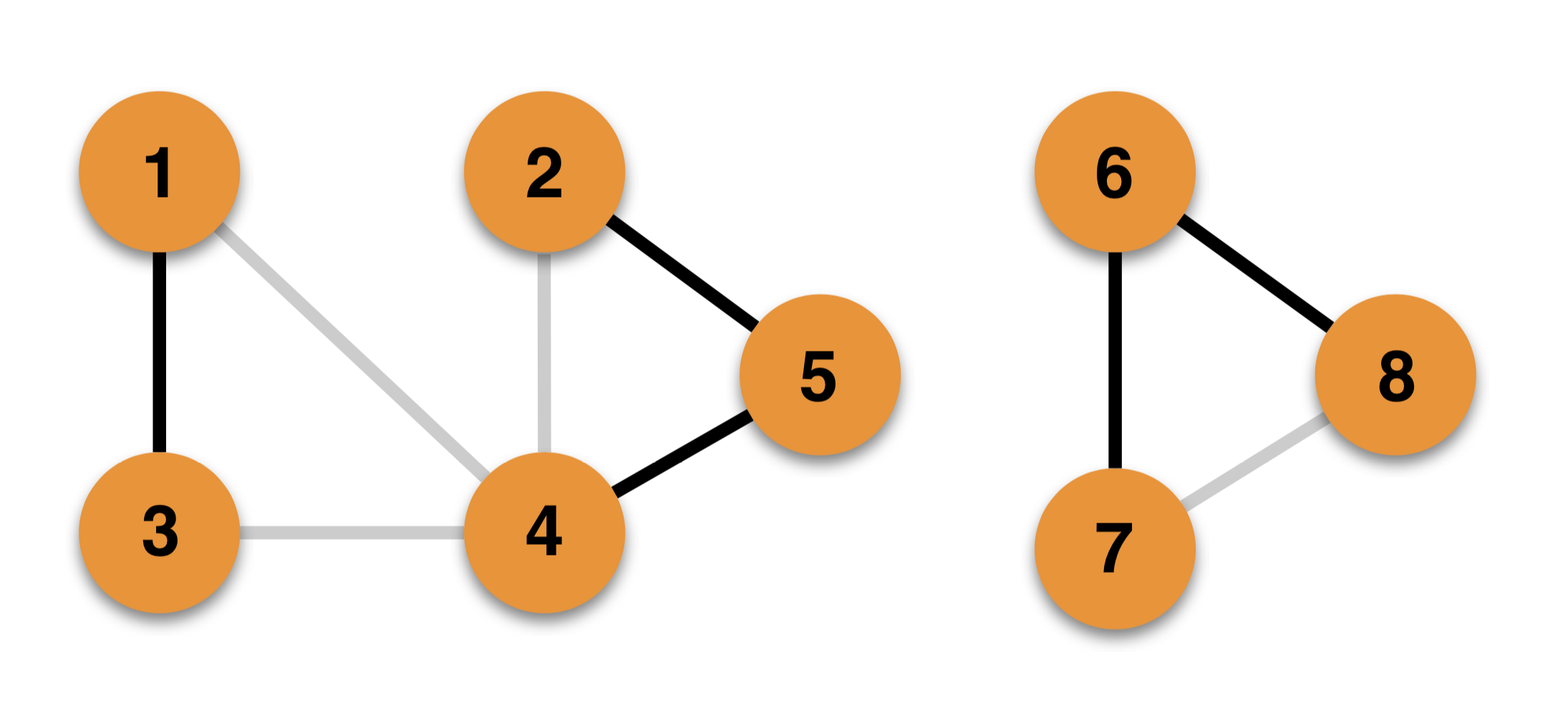
- 新边的加入使原先的图构成了「含奇数条边的环」,如下图此时若到来一条
2 - 4或7 - 8的边,均破坏了二分图的性质。此时的判断条件是:两个顶点同属于一个 Component 且两个顶点的颜色相同。 - 新边的加入使原先的图构成了「含偶数条边的环」,则图依然保持二分图的性质。此时的判断条件是:两个顶点同属于一个 Component 且两个顶点的颜色相异。
- 新边的两个顶点分属不同的 Componets,如下图此时若到来一条
1 - 4边,图依然保持二分图的性质。我们可以做简单的证明:由于之前的两个单独的 Components 均是二分图,则我们可以分别将它们的顶点划分到两个不相交的集合中{U1}、{V1}和{U2}、{V2}中且令新边(i,j)的顶点i∈ U1,j∈ V2,由此可得出由{U1}、{U2}构成的集合{U}与{V1}、{V2}构成的集合{V}不相交,未破环二分图的性质。此时的判断条件:两个顶点分属于不同的 Components。在算法实现时,我们需要将两个 Components 合并为一个 Component,即 Gelly 算法中的merge操作。需要注意的是,此时若两个顶点(已染色)颜色不同,则直接合并,若两个顶点颜色相同,则需要将其中的一个 Component 颜色反转。